Sparse matrix-vector products
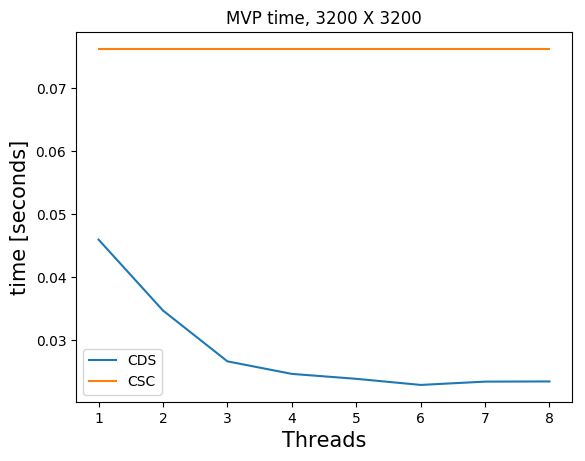
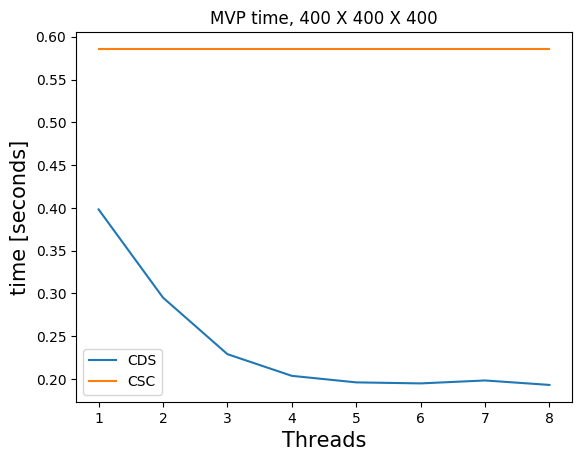
The standard native Julia sparse matrix (SparseMatrixCSC) is stored in the compressed sparse column format (CSC). Matrix-vector products with this type of matrix do not use multithreading in Julia (although there is non-Julia software that does use multiple threads and obtains small speedups).
Many of our matrices \(A\), get a banded structure when we form \(A^\top A\). A banded structure is a matrix that has a small number of diagonals with nonzero elements. For example, if \(A\) is a first-order finite-difference matrix for a 2D domain, \(A^\top A\) also has a banded structure. We store the matrices \(B = A^\top A\) in the compressed diagonal storage format (CDS) (sometimes referred to as the DIA format) if \(B \in \mathbb{R}^{N \times N}\) has a banded structure. This means we store all \(d\) nonzero diagonals as a dense matrix \(R \in \mathbb{R}^{N \times d}\) and a vector \(n \in \mathbb{R}^d\) with the indices of nonzero diagonals.
Matrix-vector products in the CDS format are faster for banded matrices and also achieve a nice speedup using multiple threads. The multi-treading is implemented in pure Julia using only a few lines of code.
Below, we compare timings for 2D and 3D models of various sizes for various number of threads on a dedicated cluster node with \(2\) CPUs per node, 10 cores per CPU (Intel Ivy Bridge 2.8 GHz E5-2680v2) and 128 GB memory per node. We show results for matrix-vector products in the CSC and CDS format for a laplacian matrix. The CSC MVPs in Julia are computed as the transpose of the matrix, which is a bit faster than with the matrix itself. The matrices \(B\) are always symmetric so we don’t need to compute additional transposes of matrices.
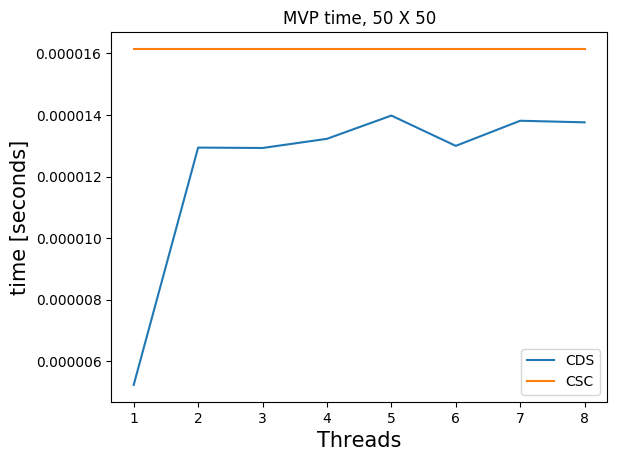
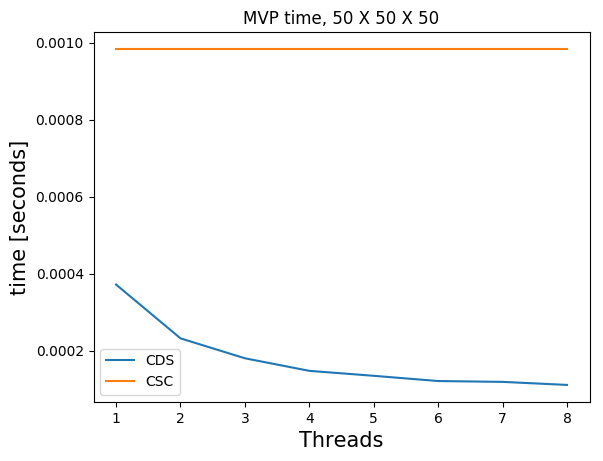
Julia) and compressed diagonal storage (CDS, our implementation). Multi-threading does not pay off for too small models.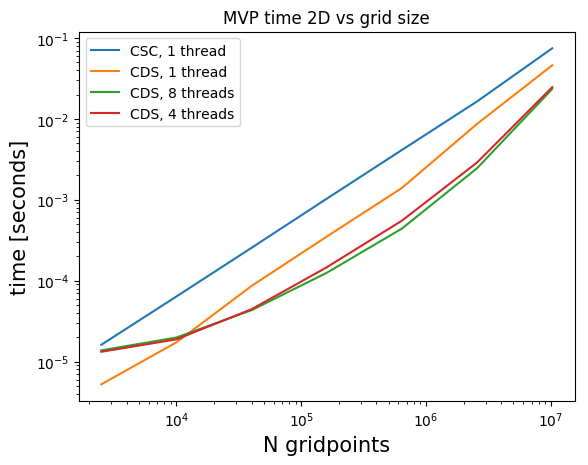
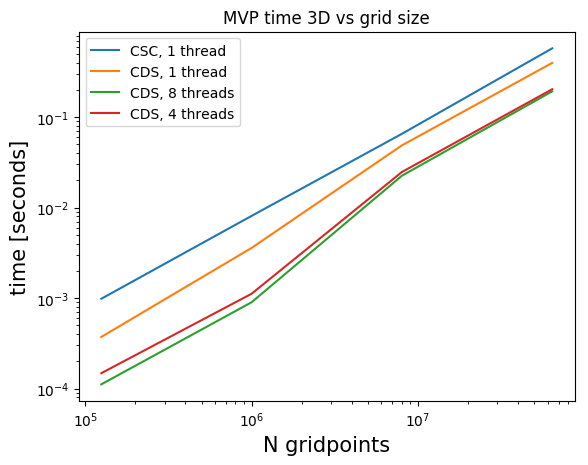
Julia) and compressed diagonal storage (CDS, our implementation).