Dr. Bas Peters

Logo

Research Scientist at Computational Geosciences Inc

View My GitHub Profile

Bas Peters

LinkedIn Google Scholar GitHub
Hi! I am a research scientist at Computational Geosciences Inc. Before, I was a research scientist at Proteic Bioscience (currently DiaGen Ai) in Vancouver BC. Previously, I was a visiting assistant professor (2020-2021) in the mathematics department at Emory University. Before that, I worked for Computational Geosciences Inc. and I was a graduate student in the SLIM group at the University of British Columbia (currently at Georgia Tech).

My research interests include

Teaching

Emory University:

Fall 2020: Linear Algebra MATH221 (all class info on Canvas)

Spring 2021: Linear Algebra MATH221 (all class info on Canvas)

Recent Publications

Please see my scholar page. for other publications.

Recent & Upcoming Presentations

Selected Presentations

Optimization and energy functions for protein design

Computational methods for training neural networks for large scale inputs

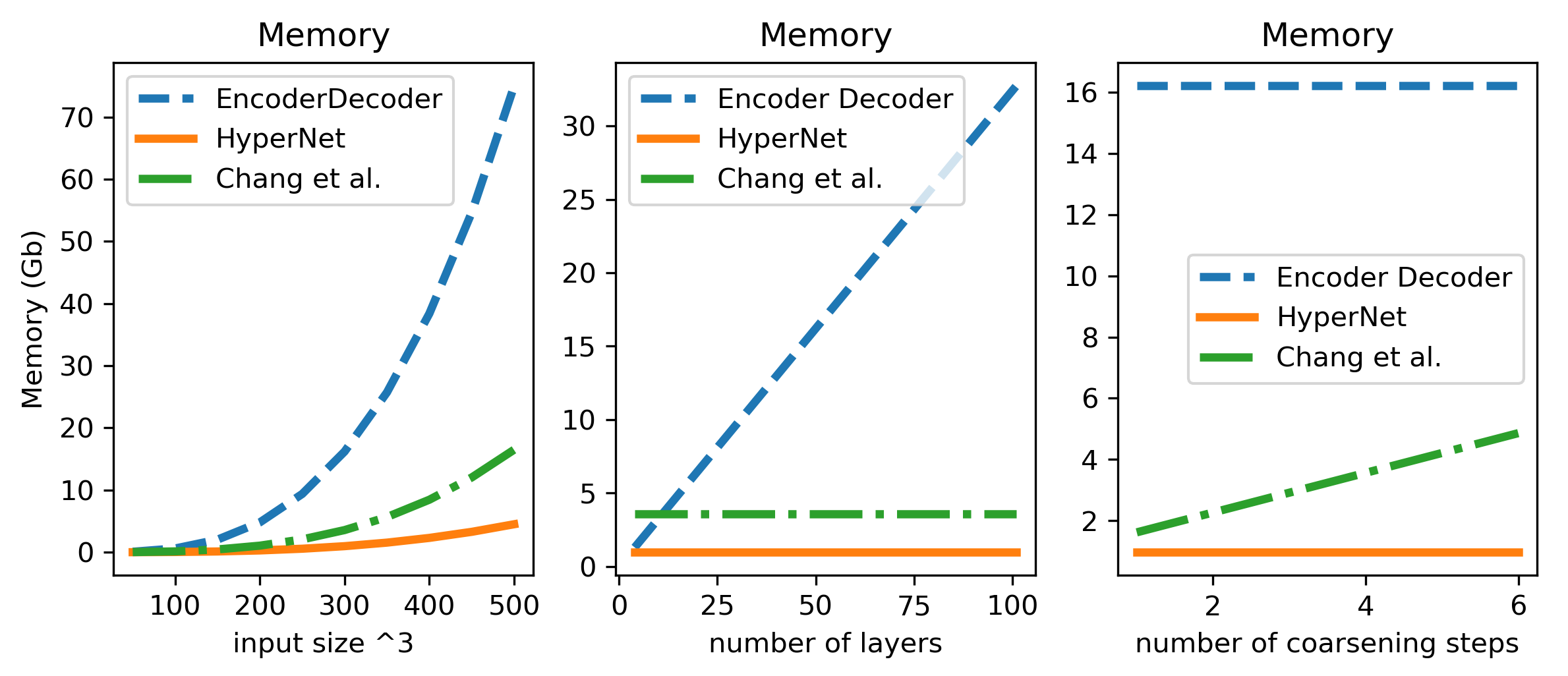
Collaborators: Keegan Lensink & Eldad Haber. Research focusses on developing fully reversible and invertible networks that have constant memory requirements as a function of network depth. This topic also includes methods for training networks in a ‘factorized’ form to reduce the memory required for weights.

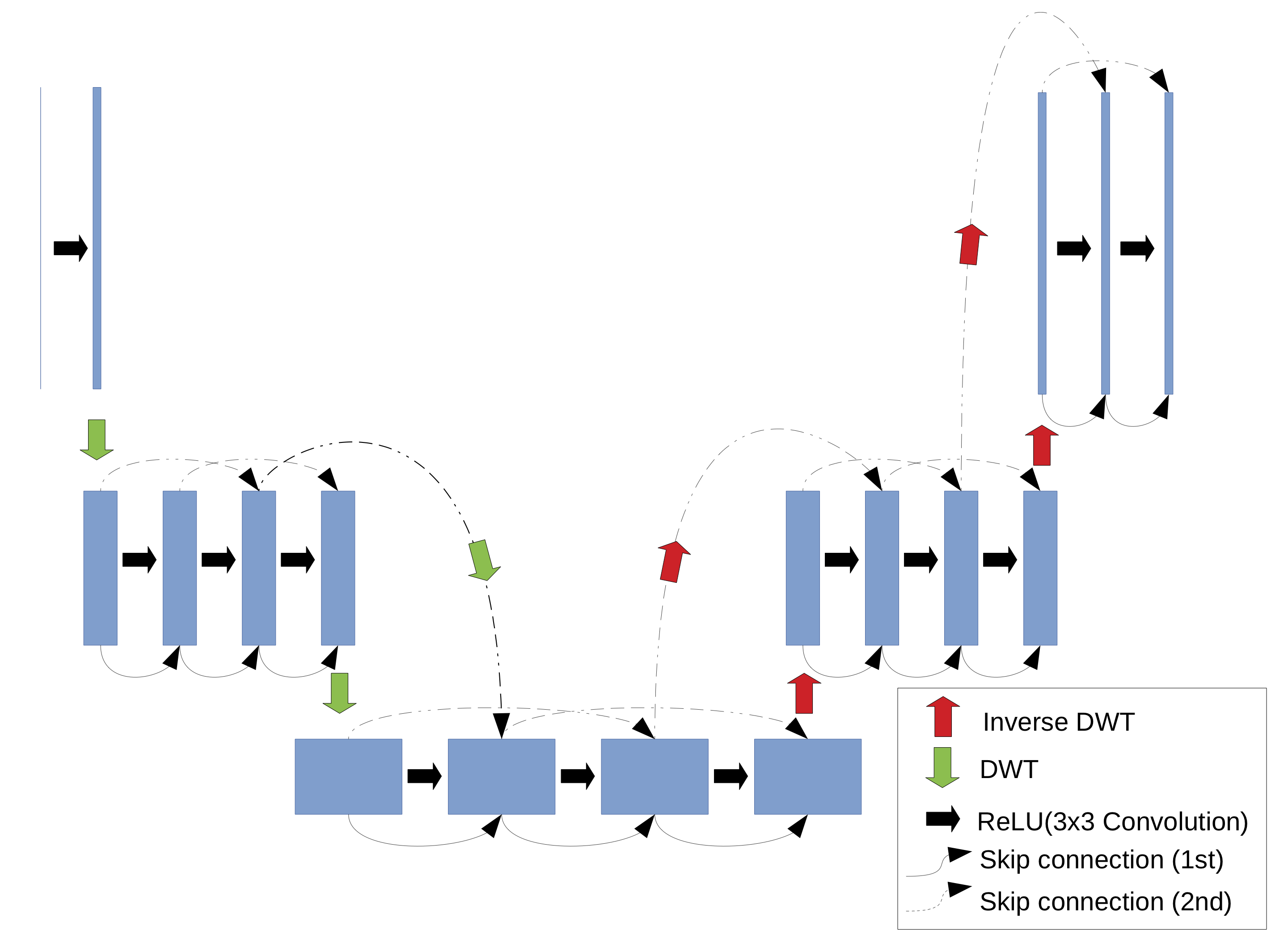
Fully Hyperbolic Convolutional Neural Networks Symmetric block-low-rank layers for fully reversible multilevel neural networks

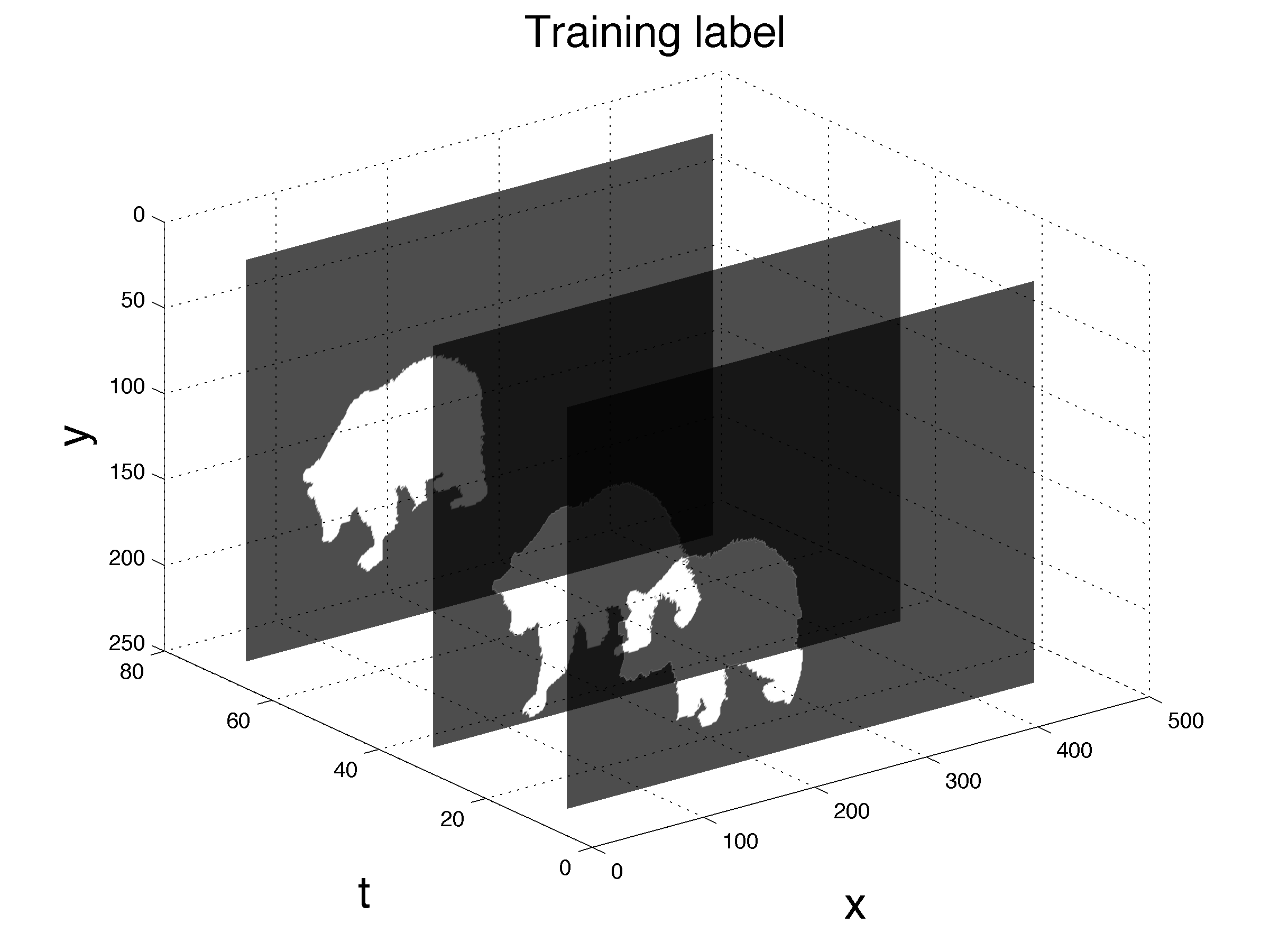
Applications include video segmentation, (time-lapse) hyperspectral land use classification and generative modeling. The low memory requirements of the fully reversible network allows us to segment a full video in one go. The following example segments a full video, based on three given slices.

Deep-learning based computer vision geoscience and remote sensing applications

Collaborators: Eldad Haber & Justin Granek. For this project we develop deep learning methods to be able to apply deep neural-networks to geoscience problems. We worked on techniques to deal with

Applications include aquifer mapping using topography, gravitational, magnetic data, as well as various geological maps and point observations of the ground truth.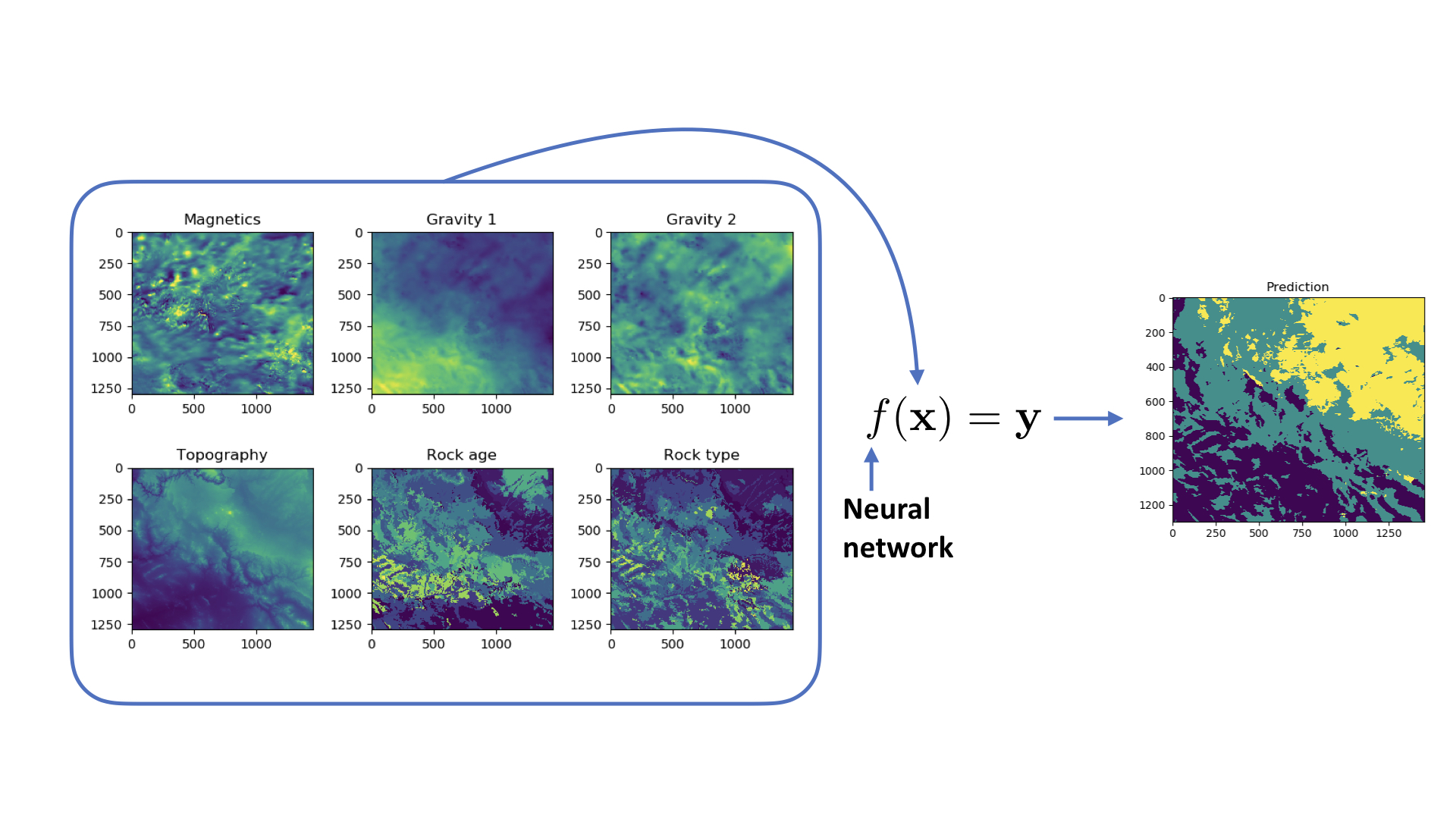
Time-lapse hyperspectral imaging maps a 4D input to a 2D maps of the suface of the earth, in terms of land-use change.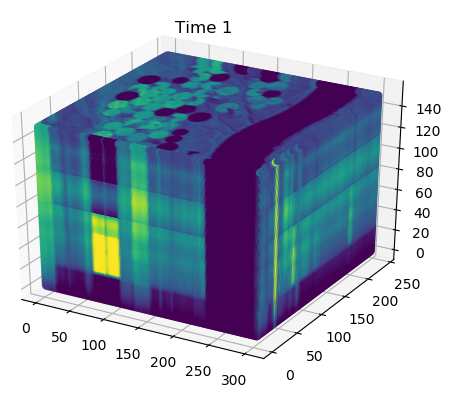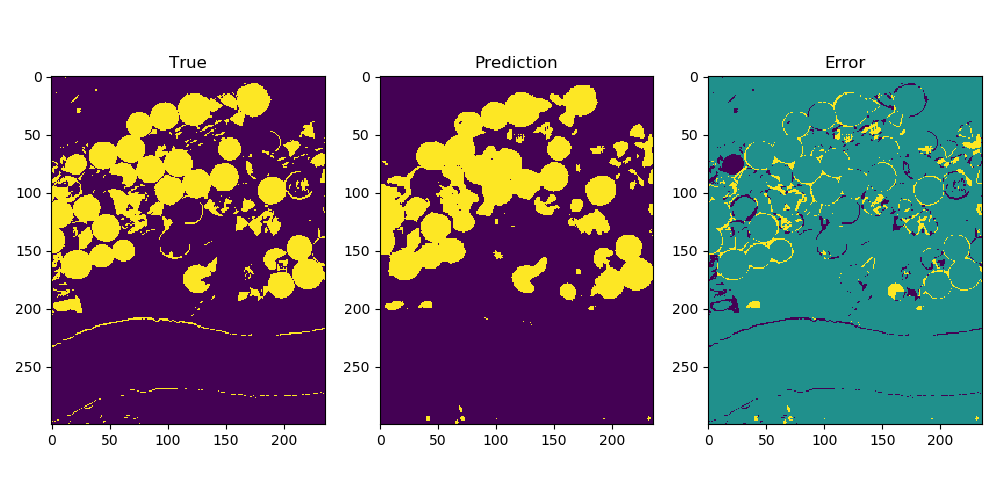

2D/3D geological model building from seismic images and borehole data (labels)

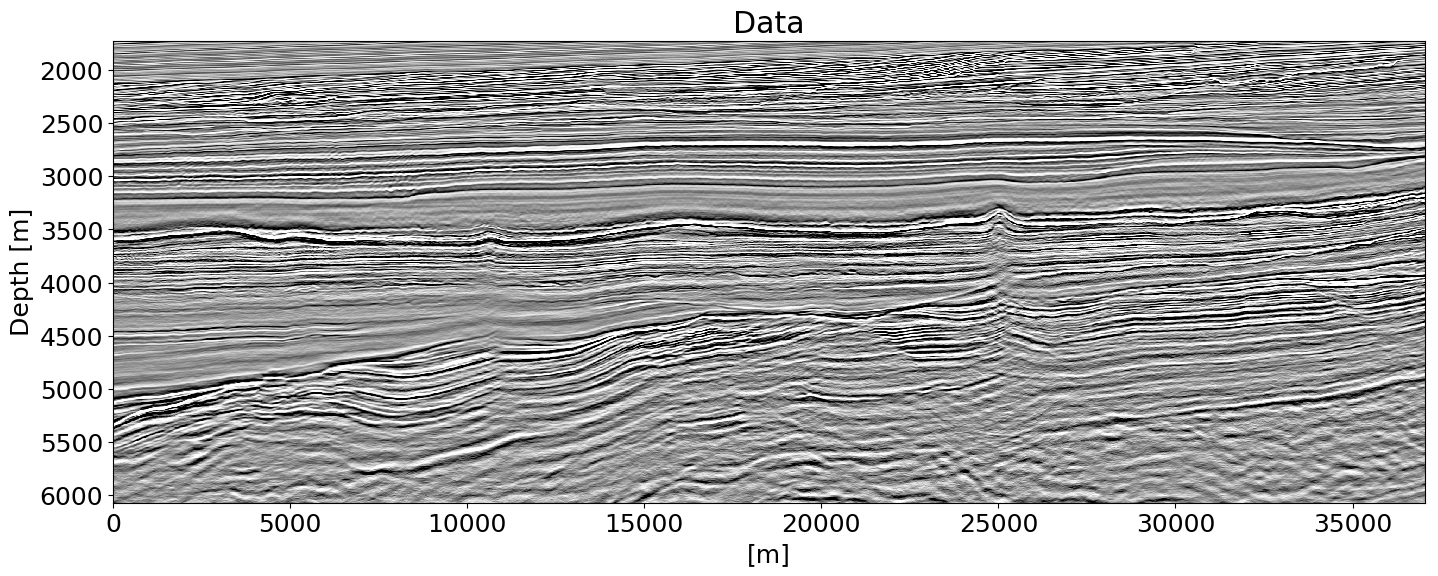
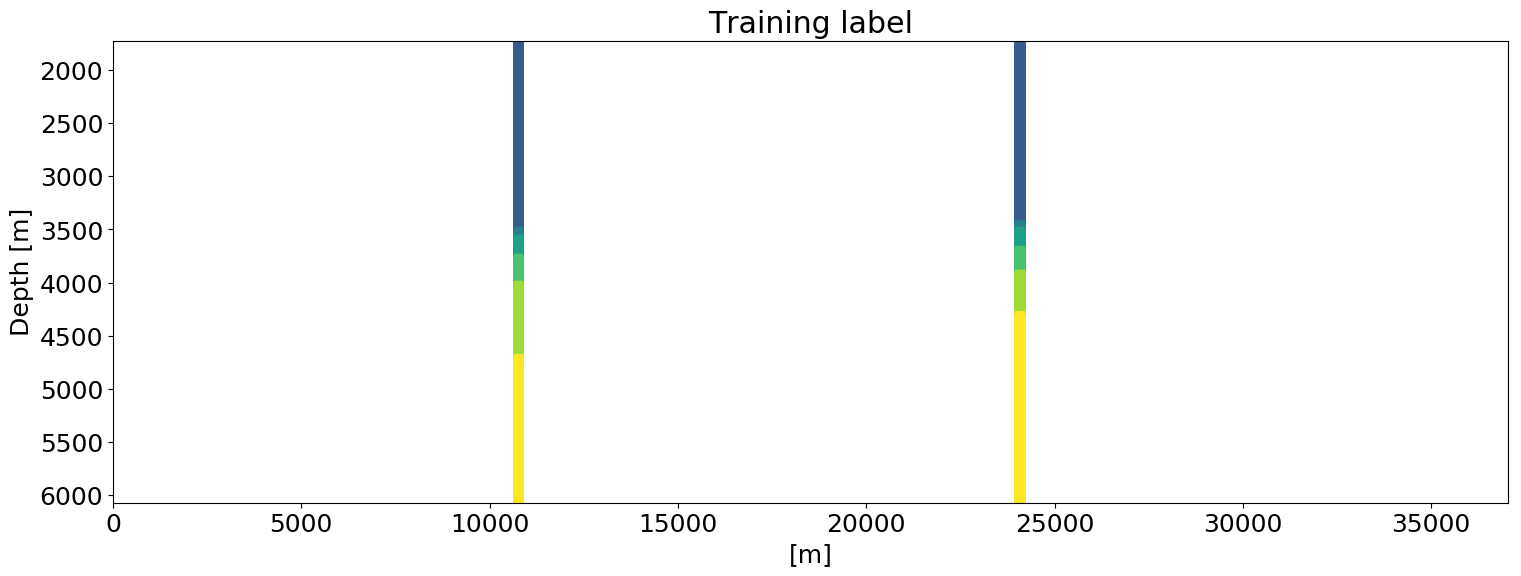
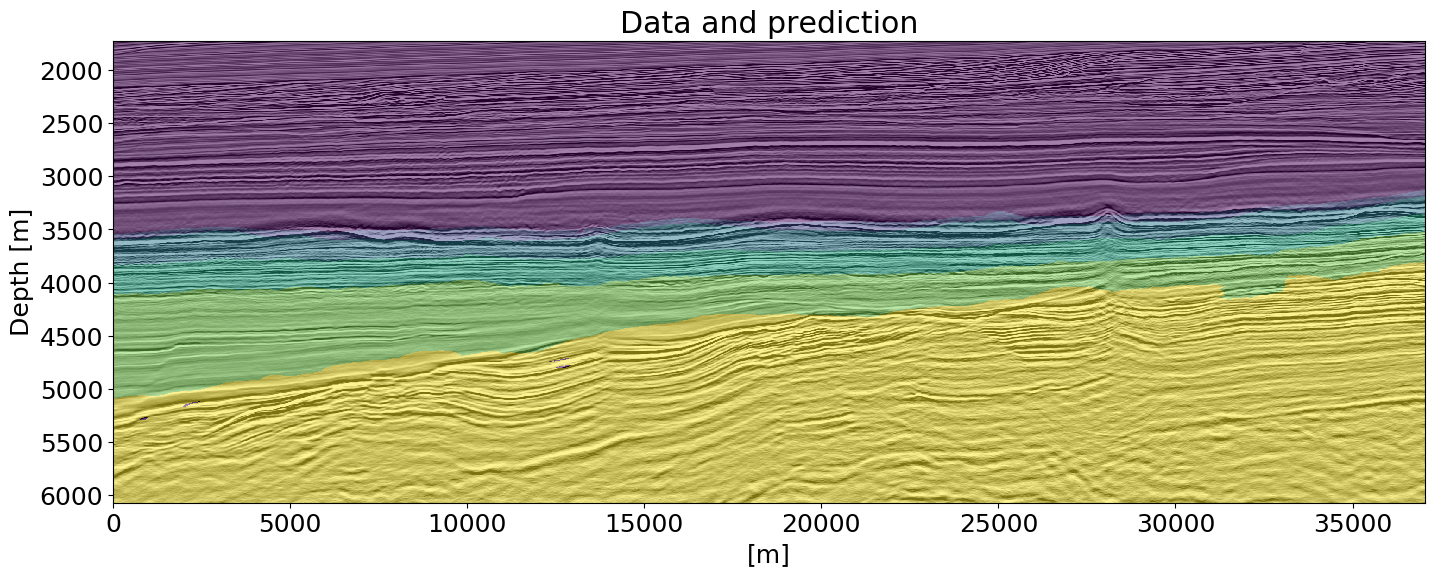
Automatic Classification of Geologic Units in Seismic Images Using Partially Interpreted Examples / arXiv

Neural-networks for geophysicists and their application to seismic data interpretation / arXiv

Does shallow geological knowledge help neural-networks to predict deep units? / arXiv

Detecting horizons (interfaces) of interest in seismic images. There are a number of training images and each has a few labels (seed points). Our method performs better than methods not based on learning, especially in areas where there are large gaps in the labels.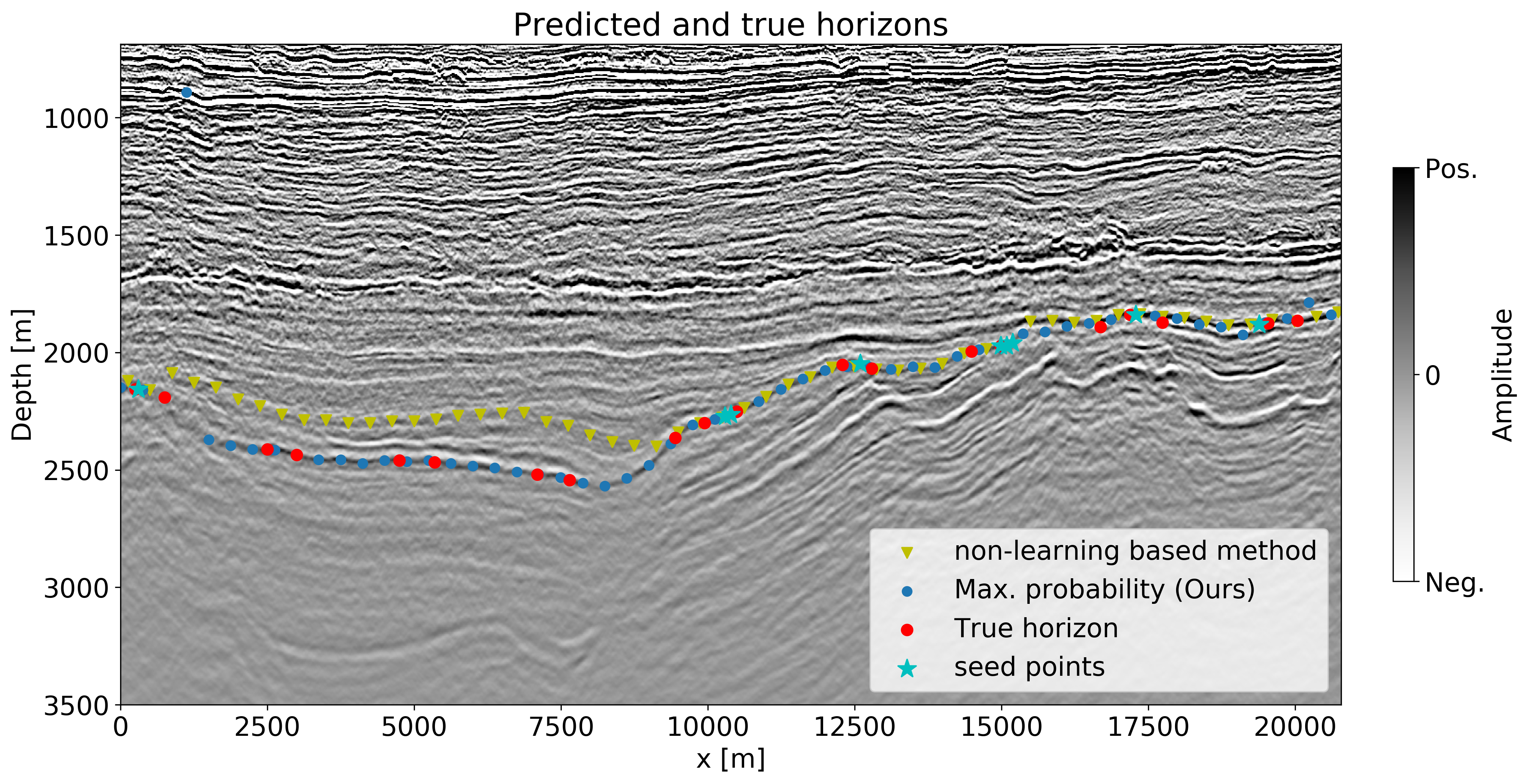

Multiresolution neural networks for tracking seismic horizons from few training images / arXiv

Constrained optimization for regularizing inverse problems & neural networks

Collaborator: Felix J. Herrmann.

We incorporate prior knowledge into the inverse problems via a projection of a vector onto an intersection of multiple convex and non-convex sets. Each sets may include a different linear operator, such as discrete derivative matrices, Fourier/DCT/wavelet/curvelet transforms. The projection approach has the advantage that each sets is defined independently of all others; no trade-off/balancing parameters are required. Julia software is available as the SetIntersectionProjection package. Applications include image/video processing and non-convex geophysical parameter estimation problems.

Reconstructing images from noisy, blurred, and missing pixels. Shows basis-pursuit denoise using wavelets, versus our method (PARSDMM): projection onto an intersection of constraint sets that were learned from examples.

In case it is difficult to describe a model/image using a set or intersection of sets as above, we can use an additive model. Therefore, we introduced a generalization of the Minkowski set, which allows us to construct a ‘complicated’ model/image from two ‘simple’ ones. We can add multiple pieces of prior knowledge about each component as well multiple constraints on their sum. In spirit, this approach generalized ideas from cartoon-texture decomposition, robust prinipal component analysis, and morphological component analysis. Julia software is available to set up constraints sets and compute the projection onto the Generalized Minkowski Set.

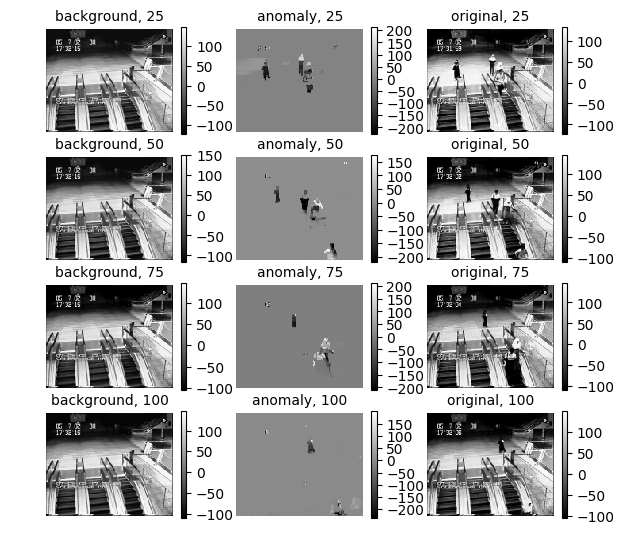
Generalized Minkowski sets for the regularization of inverse problems (preprint)

Software

SetIntersectionProjection

Generalized Minkowski Set projections

Numerical linear algebra and PDE-constrained optimization

Collaborators: Felix J. Herrmann & Tristan van Leeuwen

We investigated how and when quadratic penalty methods offer andvantages over reduced-Lagrangian (adjoint-state) methods for non-convex seismic PDE-constrained optimization problems, in terms of the quality of the solution.

Wave-equation Based Inversion with the Penalty Method-Adjoint-state Versus Wavefield-reconstruction Inversion/preprint A new take on FWI-wavefield reconstruction inversion/preprint

We also did some work in numerical linear algebra, aimed at seismic parameter estimation problems. We developed a sparse hessian approximation for quadratic-penalty method sub-problems that arise from estimating two different physical parameters simultaneously. This leads to challenges because different physical parameters can have scalings that are orders of magnitudes apart.

A sparse reduced Hessian approximation for multi-parameter wavefield reconstruction inversion/preprint

I developed a solver for block-structured least-squares problems, with slightly more rows than columns. These problems arise when solving for the states/fields when reduced quadratic-penalty methods are employed for time-harmonic PDE-constrained optimization problems. This is the first work that solves such problems in 3D and is based on a identity+low-rank factorization & Sherman-Morrison-Woodbury.

A numerical solver for least-squares sub-problems in 3D wavefield reconstruction inversion and related problem formulations/preprint

Parallel reformulation of the sequential adjoint-state method/preprint